BAEC(N)121 SOLVED QUESTION PAPER 2024
SECTION "A"
LONG ANSWER TYPE QUESTIONS
प्रश्न 01 सांख्यिकी से आप क्या समझते हैं? अर्थशास्त्र में सांख्यिकी के महत्व के बारे में वर्णन कीजिए।
सांख्यिकी का अर्थ
सांख्यिकी (Statistics) गणित की वह शाखा है जिसमें आंकड़ों का संग्रह, वर्गीकरण, विश्लेषण, प्रस्तुतीकरण और उनकी व्याख्या की जाती है। यह एक वैज्ञानिक विधि है जो विभिन्न क्षेत्रों में निर्णय लेने की प्रक्रिया को सरल और सटीक बनाती है। सांख्यिकी का प्रयोग सामाजिक विज्ञान, अर्थशास्त्र, चिकित्सा, प्रबंधन, कृषि और अन्य कई क्षेत्रों में किया जाता है।
अर्थशास्त्र में सांख्यिकी का महत्व
अर्थशास्त्र में सांख्यिकी की महत्वपूर्ण भूमिका होती है क्योंकि यह आर्थिक नीतियों, योजनाओं और पूर्वानुमानों को वैज्ञानिक आधार प्रदान करती है। इसके प्रमुख महत्व इस प्रकार हैं—
आर्थिक डेटा का संग्रह और विश्लेषण
सांख्यिकी की मदद से विभिन्न आर्थिक गतिविधियों जैसे उत्पादन, उपभोग, निवेश, आय, रोजगार, महंगाई आदि का आंकड़ों के रूप में संग्रह और विश्लेषण किया जाता है।
राष्ट्रीय आय की गणना
सांख्यिकी का उपयोग राष्ट्रीय आय, प्रति व्यक्ति आय, सकल घरेलू उत्पाद (GDP) और सकल राष्ट्रीय उत्पाद (GNP) की गणना में किया जाता है, जिससे देश की आर्थिक स्थिति का सही आकलन किया जा सकता है।
मांग और आपूर्ति का विश्लेषण
सांख्यिकी की मदद से अर्थशास्त्री किसी वस्तु की मांग और आपूर्ति के पैटर्न को समझ सकते हैं और तदनुसार नीतियां बना सकते हैं।
मुद्रास्फीति और महंगाई का अध्ययन
सांख्यिकी का उपयोग मूल्य सूचकांक, मुद्रास्फीति दर और क्रय शक्ति में बदलाव के अध्ययन में किया जाता है, जिससे सरकार आवश्यक नीतिगत सुधार कर सकती है।
वित्तीय और मौद्रिक नीतियों का निर्धारण
सरकार और केंद्रीय बैंक (जैसे भारतीय रिजर्व बैंक) आर्थिक नीतियों को निर्धारित करने के लिए सांख्यिकीय डेटा का उपयोग करते हैं, जिससे ब्याज दर, मुद्रा आपूर्ति और वित्तीय स्थिरता को नियंत्रित किया जा सके।
अर्थव्यवस्था के रुझानों का पूर्वानुमान
सांख्यिकीय विधियों की मदद से आर्थिक प्रवृत्तियों का विश्लेषण किया जाता है और भविष्य की संभावित आर्थिक स्थितियों का अनुमान लगाया जाता है।
योजनाओं और नीतियों का निर्माण
सरकार और नीति-निर्माता विभिन्न योजनाओं जैसे गरीबी उन्मूलन, बेरोजगारी निवारण, औद्योगिक विकास और कृषि सुधार योजनाओं को बनाने में सांख्यिकीय आंकड़ों का उपयोग करते हैं।
अंतरराष्ट्रीय व्यापार और अर्थव्यवस्था
सांख्यिकी के माध्यम से निर्यात, आयात, विदेशी मुद्रा भंडार और व्यापार संतुलन का अध्ययन किया जाता है, जिससे देश की आर्थिक नीतियां बनाई जाती हैं।
निष्कर्ष
सांख्यिकी अर्थशास्त्र का एक अभिन्न अंग है। यह आर्थिक गतिविधियों को मात्रात्मक रूप में प्रस्तुत कर निर्णय प्रक्रिया को अधिक प्रभावी बनाता है। सांख्यिकीय आंकड़ों के बिना कोई भी आर्थिक नीति या योजना प्रभावी रूप से नहीं बनाई जा सकती। इस प्रकार, अर्थशास्त्र में सांख्यिकी का विशेष महत्व है।
प्रश्न 02 प्राथमिक एवं द्वितीयक आंकड़े किसे कहते हैं? द्वितीयक आंकड़ों के विभिन्न स्रोतों का वर्णन कीजिए।
प्राथमिक एवं द्वितीयक आंकड़े
1. प्राथमिक आंकड़े (Primary Data)
वे आंकड़े जो किसी विशेष उद्देश्य के लिए पहली बार सीधे स्रोत से एकत्र किए जाते हैं, प्राथमिक आंकड़े कहलाते हैं। ये मूल आंकड़े होते हैं और सर्वेक्षण, साक्षात्कार, प्रश्नावली, प्रायोगिक अध्ययन आदि के माध्यम से प्राप्त किए जाते हैं।
2. द्वितीयक आंकड़े (Secondary Data)
वे आंकड़े जो पहले से किसी अन्य उद्देश्य के लिए एकत्र किए गए होते हैं और बाद में किसी अन्य अध्ययन या विश्लेषण के लिए उपयोग किए जाते हैं, द्वितीयक आंकड़े कहलाते हैं। ये आंकड़े विभिन्न सरकारी रिपोर्टों, शोध पत्रों, जनगणना रिपोर्टों, पत्रिकाओं, पुस्तकों आदि से प्राप्त किए जा सकते हैं।
द्वितीयक आंकड़ों के विभिन्न स्रोत
द्वितीयक आंकड़ों के स्रोत दो प्रकार के होते हैं—
1. प्रकाशित स्रोत (Published Sources)
इन स्रोतों से प्राप्त आंकड़े सार्वजनिक रूप से उपलब्ध होते हैं और इन्हें विभिन्न संगठनों द्वारा प्रकाशित किया जाता है। इसके प्रमुख स्रोत निम्नलिखित हैं—
सरकारी प्रकाशन – सरकार विभिन्न आर्थिक, सामाजिक और जनगणना संबंधी रिपोर्टें प्रकाशित करती है, जैसे कि राष्ट्रीय नमूना सर्वेक्षण (NSS), भारतीय रिजर्व बैंक (RBI) की रिपोर्ट, आर्थिक सर्वेक्षण आदि।
अंतरराष्ट्रीय संगठनों की रिपोर्ट – संयुक्त राष्ट्र (UN), विश्व बैंक (World Bank), अंतरराष्ट्रीय मुद्रा कोष (IMF), एशियाई विकास बैंक (ADB) आदि द्वारा प्रकाशित रिपोर्टें।
शोध पत्र और विद्वानों के अध्ययन – विश्वविद्यालयों और शोध संस्थानों द्वारा प्रकाशित शोध पत्र, जर्नल और रिपोर्टें।
व्यापारिक और औद्योगिक रिपोर्टें – विभिन्न उद्योग संगठनों, व्यापार संघों और कंपनियों द्वारा प्रकाशित वार्षिक रिपोर्टें।
अखबार और पत्रिकाएं – आर्थिक और व्यावसायिक पत्रिकाएं, जैसे कि आर्थिक एवं राजनीतिक साप्ताहिक (EPW), बिजनेस टुडे, द इकोनॉमिक टाइम्स आदि।
2. अप्रकाशित स्रोत (Unpublished Sources)
कई बार कुछ आंकड़े प्रकाशित नहीं होते हैं, लेकिन वे शोध और विश्लेषण के लिए उपयोग किए जा सकते हैं। इसके प्रमुख स्रोत हैं—
सरकारी विभागों के रिकॉर्ड – कुछ सरकारी एजेंसियां आंतरिक उपयोग के लिए आंकड़े एकत्र करती हैं, जिन्हें सार्वजनिक रूप से प्रकाशित नहीं किया जाता।
शोध संस्थानों के आंकड़े – विभिन्न शैक्षणिक और शोध संस्थानों द्वारा किए गए अध्ययन जिनकी रिपोर्टें प्रकाशित नहीं की जातीं।
कंपनियों और व्यावसायिक संगठनों के रिकॉर्ड – निजी कंपनियों और उद्योग संगठनों के आंतरिक डेटा।
व्यक्तिगत अनुसंधान और फील्ड सर्वेक्षण – कुछ विद्वानों और शोधकर्ताओं द्वारा एकत्र किए गए आंकड़े, जो व्यक्तिगत शोध में उपयोग होते हैं।
निष्कर्ष
द्वितीयक आंकड़े किसी भी शोध और आर्थिक अध्ययन के लिए महत्वपूर्ण होते हैं क्योंकि वे समय और लागत की बचत करते हैं। हालांकि, इन आंकड़ों की प्रामाणिकता और सटीकता की जांच करना आवश्यक होता है। विभिन्न स्रोतों से प्राप्त द्वितीयक आंकड़े किसी भी अध्ययन को अधिक गहराई और विश्वसनीयता प्रदान करते हैं।
प्रश्न 03 केंद्रीय प्रवृति की माप से क्या अभिप्राय है? विभिन्न प्रकार के माध्यों के गुण एवं दोषों की विवेचना कीजिए।
केंद्रीय प्रवृत्ति की माप का अभिप्राय
किसी सांख्यिकीय आंकड़ों के समूह में ऐसे मान की खोज, जो संपूर्ण आंकड़ों का प्रतिनिधित्व कर सके, केंद्रीय प्रवृत्ति की माप कहलाता है। इसे सांख्यिकीय माध्य भी कहते हैं। इसका उद्देश्य दिए गए आंकड़ों में किसी एक विशिष्ट मूल्य को चुनना होता है, जो पूरे डेटा का सार प्रस्तुत करे।
केंद्रीय प्रवृत्ति की माप के मुख्य प्रकार निम्नलिखित हैं—
गणितीय माध्य (Arithmetic Mean)
माध्यिका (Median)
बहुलक (Mode)
विभिन्न प्रकार के माध्यों के गुण एवं दोष
1. गणितीय माध्य (Arithmetic Mean)
गणितीय माध्य किसी संख्या समूह का औसत होता है। इसे निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है—
Mean=. ∑X
N
जहाँ,
∑X = सभी आंकड़ों का योग
N = आंकड़ों की कुल संख्या
गुण:
सबसे सरल और व्यापक रूप से उपयोग किया जाने वाला माप।
सभी मूल्यों को ध्यान में रखता है।
बीजगणितीय गणनाओं में उपयोगी।
दोष:
अत्यधिक बड़े या छोटे मूल्यों (outliers) से प्रभावित होता है।
जब आंकड़े असंतुलित होते हैं, तब यह भ्रामक हो सकता है।
गुणात्मक आंकड़ों पर लागू नहीं किया जा सकता।
2. माध्यिका (Median)
माध्यिका वह संख्या होती है, जो आंकड़ों को दो बराबर भागों में विभाजित करती है। यदि आंकड़ों की संख्या विषम है, तो मध्य का मान माध्यिका होता है, और यदि सम है, तो मध्य के दो मानों का औसत माध्यिका होता है।
गुण:
अपवर्तक मूल्यों (outliers) से प्रभावित नहीं होता।
असंतुलित आंकड़ों में भी सटीक परिणाम देता है।
समष्टिगत आंकड़ों में आसानी से ज्ञात किया जा सकता है।
दोष:
गणितीय गणनाओं में कठिनाई होती है।
सभी मूल्यों को ध्यान में नहीं रखता।
जब आंकड़ों की संख्या अधिक होती है, तो इसे व्यवस्थित करना कठिन हो जाता है।
3. बहुलक (Mode)
बहुलक वह संख्या होती है, जो आंकड़ों में सबसे अधिक बार प्रकट होती है।
गुण:
किसी भी प्रकार के आंकड़ों पर लागू किया जा सकता है।
व्यावहारिक निर्णयों में सहायक होता है, जैसे व्यापार, अर्थशास्त्र और बाजार विश्लेषण में।
गणना करने में आसान।
दोष:
कभी-कभी एक से अधिक बहुलक हो सकते हैं, जिससे भ्रम उत्पन्न होता है।
यदि सभी मान अलग-अलग हों, तो बहुलक निकालना कठिन हो जाता है।
बीजगणितीय गणनाओं में उपयोगी नहीं होता।
निष्कर्ष
केंद्रीय प्रवृत्ति की माप सांख्यिकीय विश्लेषण का एक महत्वपूर्ण उपकरण है। विभिन्न माध्य अपने विशिष्ट गुणों और दोषों के कारण अलग-अलग परिस्थितियों में उपयोग किए जाते हैं। गणितीय माध्य गणनात्मक दृष्टि से महत्वपूर्ण है, जबकि माध्यिका असंतुलित आंकड़ों में अधिक विश्वसनीय होती है, और बहुलक व्यावसायिक और वास्तविक जीवन की स्थितियों में अधिक उपयोगी होता है।
प्रश्न 04 नमूना विधि की प्रायिकता और गैर प्रायिकता विधियों के बारे में विस्तार से चर्चा कीजिए।
नमूना विधि (Sampling Method) सांख्यिकी में एक महत्वपूर्ण तकनीक है, जिसके द्वारा संपूर्ण जनसंख्या (Population) से कुछ इकाइयों को चयनित करके अध्ययन किया जाता है। यह विधि अनुसंधान को प्रभावी, समय-बचत करने वाली और व्यावहारिक बनाती है।
नमूना विधियों को दो प्रमुख भागों में विभाजित किया जाता है—
प्रायिकता नमूना विधि (Probability Sampling Method)
गैर-प्रायिकता नमूना विधि (Non-Probability Sampling Method)
1. प्रायिकता नमूना विधि (Probability Sampling Method)
इस विधि में प्रत्येक इकाई को चुने जाने का एक ज्ञात और समान अवसर होता है। इसमें पूर्वाग्रह (Bias) की संभावना कम होती है और प्राप्त परिणाम संपूर्ण जनसंख्या के लिए अधिक विश्वसनीय होते हैं।
प्रमुख प्रकार
सरल यादृच्छिक नमूना (Simple Random Sampling)
प्रत्येक इकाई को समान रूप से चुने जाने का अवसर मिलता है।
यह कंप्यूटर सॉफ्टवेयर या लॉटरी पद्धति द्वारा किया जाता है।
उदाहरण: यदि किसी विश्वविद्यालय के छात्रों में से 100 छात्रों को यादृच्छिक रूप से चुना जाता है, तो यह सरल यादृच्छिक नमूना होगा।
स्ट्रैटिफाइड नमूना (Stratified Sampling)
जनसंख्या को विभिन्न उप-समूहों (Strata) में विभाजित किया जाता है और प्रत्येक समूह से आनुपातिक रूप से नमूने लिए जाते हैं।
यह तब उपयोगी होता है जब जनसंख्या विषम होती है।
उदाहरण: किसी कंपनी के कर्मचारियों को अनुभव के आधार पर वर्गीकृत करके नमूने लेना।
सिस्टेमेटिक नमूना (Systematic Sampling)
इसमें किसी निश्चित क्रम (Regular Interval) के अनुसार नमूना चुना जाता है।
उदाहरण: यदि 500 व्यक्तियों में से प्रत्येक 10वें व्यक्ति को चुना जाए, तो यह सिस्टेमेटिक नमूना कहलाएगा।
क्लस्टर नमूना (Cluster Sampling)
इसमें संपूर्ण जनसंख्या को छोटे-छोटे समूहों (Clusters) में विभाजित किया जाता है और यादृच्छिक रूप से कुछ समूहों का चयन किया जाता है।
यह तब उपयोगी होता है जब जनसंख्या भौगोलिक रूप से विस्तृत हो।
उदाहरण: किसी जिले के स्कूलों का चयन करके उन स्कूलों में अध्ययन करना।
2. गैर-प्रायिकता नमूना विधि (Non-Probability Sampling Method)
इस विधि में प्रत्येक इकाई को समान अवसर नहीं मिलता है और चयन प्रक्रिया शोधकर्ता की पसंद या सुविधा पर निर्भर करती है। यह विधि सरल और त्वरित होती है, लेकिन इसमें पूर्वाग्रह (Bias) की संभावना अधिक होती है।
प्रमुख प्रकार
सुविधा नमूना (Convenience Sampling)
इसमें नमूना शोधकर्ता की सुविधा के अनुसार चुना जाता है।
यह सबसे सरल और कम लागत वाली विधि है।
उदाहरण: किसी मॉल में आने वाले ग्राहकों से तुरंत उपलब्ध उत्तरदाताओं का चयन करना।
उद्देश्यपूर्ण नमूना (Purposive Sampling)
इसमें केवल उन्हीं इकाइयों का चयन किया जाता है, जो शोध के उद्देश्य के लिए सबसे उपयुक्त होती हैं।
यह तब उपयोगी होता है जब विशेष जानकारी वाले व्यक्तियों की आवश्यकता होती है।
उदाहरण: किसी विशेष बीमारी पर शोध के लिए केवल प्रभावित रोगियों का चयन।
कोटा नमूना (Quota Sampling)
इसमें जनसंख्या को विभिन्न वर्गों में विभाजित किया जाता है और प्रत्येक वर्ग से एक निश्चित संख्या में नमूने लिए जाते हैं।
यह स्ट्रैटिफाइड नमूना विधि के समान होता है, लेकिन इसमें इकाइयों का चयन यादृच्छिक नहीं होता।
उदाहरण: किसी सर्वेक्षण में विभिन्न आयु वर्गों से आनुपातिक रूप से उत्तरदाता चुनना।
स्नोबॉल नमूना (Snowball Sampling)
इसमें एक उत्तरदाता से अन्य उत्तरदाताओं का सुझाव लेकर नए उत्तरदाता जोड़े जाते हैं।
यह विधि तब उपयोगी होती है जब लक्षित जनसंख्या खोजना कठिन हो।
उदाहरण: किसी दुर्लभ बीमारी से ग्रसित रोगियों का अध्ययन।
निष्कर्ष
प्रायिकता नमूना विधि अधिक वैज्ञानिक और निष्पक्ष होती है, जबकि गैर-प्रायिकता विधि त्वरित और लागत प्रभावी होती है। शोध के उद्देश्य और संसाधनों के आधार पर उचित विधि का चयन किया जाता है। यदि निष्कर्षों की सटीकता और निष्पक्षता महत्वपूर्ण है, तो प्रायिकता विधियों को प्राथमिकता दी जानी चाहिए, जबकि व्यावहारिकता और समय की सीमाओं को ध्यान में रखते हुए गैर-प्रायिकता विधियों का उपयोग किया जाता है।
प्रश्न 05 पृथुशीर्षत्व की व्याख्या कीजिए। विषमता और पृथुशीर्षत्व में अंतर स्पष्ट कीजिए।
पृथुशीर्षत्व की व्याख्या
पृथुशीर्षत्व (Kurtosis) किसी सांख्यिकीय वितरण के चोटी (peak) की ऊँचाई और पूंछों (tails) की मोटाई को मापने की एक पद्धति है। यह दर्शाता है कि कोई वितरण सामान्य वितरण (Normal Distribution) की तुलना में अधिक चपटा (Flat) या अधिक नुकीला (Peaked) है या नहीं।
पृथुशीर्षत्व के प्रकार
लीप्टोकर्टिक (Leptokurtic, β₂ > 3)
इस प्रकार के वितरण में चोटी अधिक ऊँची और संकरी होती है।
डेटा बिंदु अधिक केंद्रित होते हैं, और एक्सट्रीम वैल्यू (outliers) अधिक होती हैं।
उदाहरण: परीक्षाओं में ऐसे अंक वितरण, जहाँ अधिकांश छात्र उच्च अंक प्राप्त करते हैं।
मेसोकर्टिक (Mesokurtic, β₂ = 3)
यह सामान्य वितरण (Normal Distribution) के समान होता है।
इसकी चोटी मध्यम ऊँचाई की होती है, और पूंछें न तो बहुत मोटी होती हैं, न ही बहुत पतली।
उदाहरण: किसी बड़े जनसमूह में बुद्धि स्तर का वितरण।
प्लैटिकोर्टिक (Platykurtic, β₂ < 3)
इसमें चोटी चपटी होती है और पूंछें पतली होती हैं।
डेटा बिंदु अधिक फैले होते हैं, और आउटलायर्स की संख्या कम होती है।
उदाहरण: यादृच्छिक रूप से चुने गए लोगों के खेल प्रदर्शन का स्कोर वितरण।
विषमता और पृथुशीर्षत्व में अंतर
आधारविषमता (Skewness)पृथुशीर्षत्व (Kurtosis)अर्थवितरण की असंतुलनता को दर्शाता है, यानी वितरण का एक तरफ झुका होना।वितरण की चोटी की ऊँचाई और पूंछ की मोटाई को मापता है।प्रकारधनात्मक (Positive), ऋणात्मक (Negative), और शून्य (Zero)लीप्टोकर्टिक, मेसोकर्टिक, प्लैटिकोर्टिकक्या मापता है?डेटा किस ओर फैला हुआ है (बाएँ या दाएँ)डेटा कितना केंद्रित या फैला हुआ हैप्रभावऔसत (Mean) को प्रभावित करता है, जिससे माध्यिका (Median) और बहुलक (Mode) बदल सकते हैं।वितरण की ऊँचाई और पूंछों को प्रभावित करता है, लेकिन औसत पर सीधा प्रभाव नहीं डालता।उदाहरणआय वितरण: यदि अधिकतर लोग कम आय अर्जित करते हैं, तो यह धनात्मक विषमता होगी।परीक्षा परिणाम: यदि अधिकतर छात्र मध्यम अंक प्राप्त करते हैं, तो यह मेसोकर्टिक होगा।
निष्कर्ष
विषमता और पृथुशीर्षत्व दोनों वितरण के स्वरूप को समझने में सहायक होते हैं। विषमता यह बताती है कि वितरण असंतुलित है या संतुलित, जबकि पृथुशीर्षत्व यह मापता है कि वितरण कितना नुकीला या चपटा है। सांख्यिकी और अर्थशास्त्र में इन दोनों का विश्लेषण डेटा की सटीक व्याख्या और निष्कर्ष निकालने में महत्वपूर्ण भूमिका निभाता है।
प्रश्न 01 समग्र अनुसंधान एवं न्यादर्श अनुसंधान से आप क्या समझते हैं? दोनों के बीच अंतर स्पष्ट कीजिए।
समग्र अनुसंधान एवं न्यादर्श अनुसंधान का परिचय
अनुसंधान एक व्यवस्थित प्रक्रिया है, जिसके माध्यम से किसी विषय या समस्या का विश्लेषण कर निष्कर्ष निकाला जाता है। अनुसंधान को विभिन्न प्रकारों में विभाजित किया जा सकता है, जिनमें समग्र अनुसंधान और न्यादर्श अनुसंधान महत्वपूर्ण स्थान रखते हैं।
समग्र अनुसंधान
समग्र अनुसंधान वह प्रक्रिया है जिसमें पूरे जनसंख्या समूह या किसी बड़े समुदाय का अध्ययन किया जाता है। इसमें सभी इकाइयों से डाटा संग्रहित किया जाता है ताकि व्यापक और सटीक निष्कर्ष निकाले जा सकें। यह अनुसंधान तब उपयोगी होता है जब संपूर्ण जनसंख्या पर आधारित सटीक जानकारी प्राप्त करनी हो। हालांकि, यह महंगा, समय-साध्य और जटिल होता है, क्योंकि इसमें बहुत अधिक संसाधनों की आवश्यकता होती है।
न्यादर्श अनुसंधान
न्यादर्श अनुसंधान में पूरे जनसंख्या समूह का अध्ययन करने के बजाय उसके एक छोटे प्रतिनिधि समूह (न्यादर्श) का अध्ययन किया जाता है। इस विधि में वैज्ञानिक रूप से चयनित नमूने के आधार पर पूरे समूह के बारे में निष्कर्ष निकाले जाते हैं। यह अनुसंधान कम खर्चीला, समय बचाने वाला और व्यावहारिक होता है, लेकिन इसकी सटीकता इस पर निर्भर करती है कि चयनित न्यादर्श सही तरीके से चुना गया है या नहीं।
समग्र अनुसंधान और न्यादर्श अनुसंधान के बीच अंतर
समग्र अनुसंधान और न्यादर्श अनुसंधान के बीच मुख्य अंतर यह है कि समग्र अनुसंधान में पूरे जनसंख्या समूह का अध्ययन किया जाता है, जबकि न्यादर्श अनुसंधान में केवल एक छोटे हिस्से का अध्ययन कर निष्कर्ष निकाला जाता है। समग्र अनुसंधान अधिक सटीक और व्यापक होता है, लेकिन इसमें अधिक समय और संसाधन लगते हैं, जबकि न्यादर्श अनुसंधान तुलनात्मक रूप से तेज़ और सस्ता होता है, किंतु उसमें संभावित त्रुटियां हो सकती हैं।
इन दोनों अनुसंधान विधियों का उपयोग अलग-अलग परिस्थितियों में किया जाता है। यदि संसाधन और समय की कोई सीमा न हो और पूर्ण सटीकता आवश्यक हो, तो समग्र अनुसंधान उपयुक्त होता है। वहीं, जब सीमित संसाधनों में त्वरित और व्यावहारिक निष्कर्ष निकालने की आवश्यकता होती है, तो न्यादर्श अनुसंधान को प्राथमिकता दी जाती है।
प्रश्न 02 बिंदुरेखीय प्रदर्शन क्या है? चित्रों या बिंदुरेखीय प्रदर्शन की उपयोगिता स्पष्ट कीजिए।
बिंदुरेखीय प्रदर्शन का अर्थ
बिंदुरेखीय प्रदर्शन (Vector Display) एक ग्राफिकल प्रस्तुतीकरण तकनीक है जिसमें छवियों या आकृतियों को बिंदुओं और रेखाओं के माध्यम से प्रदर्शित किया जाता है। यह तकनीक कंप्यूटर ग्राफिक्स, इंजीनियरिंग डिज़ाइन, आर्किटेक्चर और वैज्ञानिक डाटा विश्लेषण में महत्वपूर्ण भूमिका निभाती है। इसमें किसी वस्तु या आकृति को गणितीय समीकरणों के आधार पर बनाया जाता है, जिससे उसका आकार, रूप, और गुणवत्ता बिना विकृत हुए बढ़ाई या घटाई जा सकती है।
बिंदुरेखीय प्रदर्शन की विशेषताएँ
गुणवत्ता और स्पष्टता – यह उच्च गुणवत्ता वाली ग्राफिक्स प्रदान करता है, क्योंकि यह पिक्सेल-आधारित (रैस्टर) छवियों की तरह धुंधला नहीं होता।
मापनीयता – बिंदुरेखीय चित्रों को किसी भी आकार में परिवर्तित किया जा सकता है, फिर भी उनकी स्पष्टता बनी रहती है।
छोटा फ़ाइल आकार – यह छवियाँ आमतौर पर कम स्थान लेती हैं क्योंकि वे केवल गणितीय सूत्रों पर आधारित होती हैं।
संशोधन में आसानी – इसमें बनाए गए चित्रों को आसानी से संपादित और परिवर्तित किया जा सकता है।
तेज़ रेंडरिंग – बिंदुरेखीय ग्राफिक्स कम संसाधनों में बेहतर प्रदर्शन करते हैं, जिससे ग्राफिक्स डिजाइनिंग में इन्हें प्राथमिकता दी जाती है।
बिंदुरेखीय प्रदर्शन की उपयोगिता
ग्राफिक्स डिज़ाइन और एनीमेशन – बैनर, पोस्टर, लोगो और एनीमेशन निर्माण में बिंदुरेखीय ग्राफिक्स का व्यापक उपयोग होता है।
इंजीनियरिंग और आर्किटेक्चर – CAD (Computer-Aided Design) सॉफ्टवेयर में तकनीकी ड्रॉइंग, मॉडलिंग और डिज़ाइन के लिए बिंदुरेखीय ग्राफिक्स का उपयोग किया जाता है।
वैज्ञानिक डाटा विज़ुअलाइज़ेशन – सांख्यिकीय और गणितीय डाटा को चित्रों के माध्यम से समझाने में यह तकनीक सहायक होती है।
वीडियो गेम और वर्चुअल रियलिटी – गेम डिज़ाइन और इंटरैक्टिव ग्राफिक्स में बिंदुरेखीय चित्रों का उपयोग किया जाता है।
प्रकाशन और मुद्रण उद्योग – पुस्तकों, पत्रिकाओं, विज्ञापनों और अन्य मुद्रित सामग्री में उच्च-गुणवत्ता वाली छवियों के लिए यह तकनीक उपयुक्त होती है।
बिंदुरेखीय प्रदर्शन तकनीक डिजिटल ग्राफिक्स के क्षेत्र में एक अत्यंत उपयोगी प्रणाली है, जो न केवल चित्रों की स्पष्टता बनाए रखती है, बल्कि इसे विभिन्न अनुप्रयोगों में भी कुशलतापूर्वक उपयोग किया जा सकता है।
प्रश्न 03 विषमता से क्या अभिप्राय है? इसके जांच कैसे करें।
विषमता का अभिप्राय
विषमता (Skewness) सांख्यिकी में एक महत्वपूर्ण अवधारणा है, जिसका अर्थ है किसी वितरण (डिस्ट्रिब्यूशन) का संतुलन या असंतुलन। यह किसी डेटा सेट के माध्य (Mean), माध्यिका (Median) और बहुलक (Mode) के आपसी संबंध को दर्शाता है और यह बताता है कि डेटा किस दिशा में झुका हुआ है।
यदि कोई वितरण पूर्णतः संतुलित होता है, तो वह सामान्य वितरण (Normal Distribution) कहलाता है, जिसमें माध्य, माध्यिका और बहुलक समान होते हैं। लेकिन जब वितरण असंतुलित होता है, तो उसे विषम (Skewed) कहा जाता है।
विषमता के प्रकार
धनात्मक विषमता (Positively Skewed Distribution) – जब वितरण का लंबा भाग (Tail) दाईं ओर होता है, यानी बड़े मान अधिक होते हैं, तो इसे धनात्मक विषमता कहते हैं। इसमें माध्य > माध्यिका > बहुलक होता है।
ऋणात्मक विषमता (Negatively Skewed Distribution) – जब वितरण का लंबा भाग बाईं ओर होता है, यानी छोटे मान अधिक होते हैं, तो इसे ऋणात्मक विषमता कहते हैं। इसमें माध्य < माध्यिका < बहुलक होता है।
विषमता की जांच करने के तरीके
ग्राफिकल विधि –
Histogram: यदि ग्राफ का लंबा भाग दाईं ओर खिंचा हो, तो धनात्मक विषमता होती है। यदि यह बाईं ओर झुका हो, तो ऋणात्मक विषमता होती है।
Box Plot: इसमें विषमता को क्वार्टाइल्स के फैलाव से पहचाना जाता है।
माध्य, माध्यिका और बहुलक की तुलना –
यदि माध्य, माध्यिका से अधिक हो, तो वितरण धनात्मक विषम होता है।
यदि माध्य, माध्यिका से कम हो, तो वितरण ऋणात्मक विषम होता है।
विषमता गुणांक (Coefficient of Skewness) –
पीयरसन का गुणांक (Pearson’s Coefficient of Skewness):
यदि परिणाम धनात्मक हो, तो वितरण धनात्मक विषम है। यदि ऋणात्मक हो, तो वितरण ऋणात्मक विषम है।
मोरीस और कुर्टोसिस विधि –
विषमता को तीसरे केंद्रीय आघूर्ण (Third Central Moment) से मापा जाता है। यदि तीसरा आघूर्ण धनात्मक है, तो धनात्मक विषमता होती है, और यदि ऋणात्मक है, तो ऋणात्मक विषमता होती है।
निष्कर्ष
विषमता किसी वितरण के झुकाव को मापने का एक महत्वपूर्ण साधन है। यह सांख्यिकीय डेटा के विश्लेषण और व्याख्या में सहायता करता है, जिससे आर्थिक, सामाजिक और वैज्ञानिक अनुसंधानों में इसका व्यापक उपयोग किया जाता है।
प्रश्न 04 द्विपद तथा सामान्य वितरण की विशेषताएं बताइए।
द्विपद वितरण की विशेषताएँ
केवल दो संभावित परिणाम – प्रत्येक परीक्षण में दो ही संभावित परिणाम होते हैं, जिन्हें सफलता (Success) और असफलता (Failure) कहा जाता है।
निश्चित संख्या में परीक्षण – कुल परीक्षणों (n) की संख्या पहले से तय होती है।
स्वतंत्र घटनाएँ – प्रत्येक परीक्षण की घटना अन्य परीक्षणों से स्वतंत्र होती है।
नियत संभावना – प्रत्येक परीक्षण में सफलता की संभावना (p) नियत रहती है, और असफलता की संभावना (q = 1 - p) होती है।
संभाव्यता वितरण – किसी विशेष संख्या में सफलताओं (x) की संभावना निम्नलिखित सूत्र से प्राप्त की जाती है:
गोलाकार ग्राफ़ – द्विपद वितरण का ग्राफ छोटे n के लिए असमान्य हो सकता है, लेकिन बड़े n पर यह सामान्य वितरण के समान दिखने लगता है।
सामान्य वितरण की विशेषताएँ
घंटी के आकार का ग्राफ – सामान्य वितरण का ग्राफ घंटी के आकार का होता है, जिसे गॉसियन कर्व (Gaussian Curve) भी कहा जाता है।
माध्य, माध्यिका और बहुलक समान होते हैं – सामान्य वितरण में ये तीनों एक ही बिंदु पर होते हैं।
संपूर्ण संख्या रेखा पर फैला होता है – यह वितरण
−
∞
−∞ से
+
∞
+∞ तक फैला होता है।
सामान्यीकृत वितरण – इसमें 68% डेटा माध्य के एक मानक विचलन के भीतर, 95% दो मानक विचलनों के भीतर, और 99.7% तीन मानक विचलनों के भीतर होता है।
संपSymmetric – यह वितरण दाएं और बाएं दोनों तरफ समान होता है।
संभावना घनत्व फलन (PDF) – सामान्य वितरण को निम्नलिखित समीकरण से दर्शाया जाता है:
जहाँ,
𝜇
μ माध्य और
𝜎
σ मानक विचलन है।
द्विपद वितरण सीमित परीक्षणों के साथ दो संभावनाओं वाले प्रयोगों के लिए उपयोगी है, जबकि सामान्य वितरण बड़े डेटा सेटों में प्राकृतिक घटनाओं और सांख्यिकीय विश्लेषण के लिए उपयुक्त होता है।
प्रश्न 06 वर्गीकरण एवं सारणीयन में अंतर स्पष्ट कीजिए।
वर्गीकरण एवं सारणीयन में अंतर
वर्गीकरण और सारणीयन दोनों ही सांख्यिकीय विश्लेषण की महत्वपूर्ण प्रक्रियाएँ हैं, जिनका उद्देश्य डाटा को व्यवस्थित करना और उसे अधिक स्पष्ट रूप से प्रस्तुत करना है। हालांकि, दोनों के कार्य और प्रयोजन अलग-अलग होते हैं।
वर्गीकरण का अर्थ
वर्गीकरण वह प्रक्रिया है जिसमें किसी दिए गए डाटा को उसके लक्षणों, गुणों या विशेषताओं के आधार पर विभिन्न वर्गों या समूहों में बांटा जाता है। यह डाटा के अध्ययन और विश्लेषण को आसान बनाता है।
वर्गीकरण की विशेषताएँ
समानताओं के आधार पर डाटा को समूहों में बांटना।
गुणात्मक और मात्रात्मक दोनों डाटा पर लागू होता है।
आंकड़ों को व्यवस्थित और समझने योग्य बनाता है।
भविष्य में तुलना और विश्लेषण को आसान बनाता है।
सारणीयन का अर्थ
सारणीयन वह प्रक्रिया है जिसमें डाटा को सारणी (टेबल) के रूप में व्यवस्थित किया जाता है ताकि उसे अधिक स्पष्टता और सरलता से प्रस्तुत किया जा सके। इसमें डाटा को पंक्तियों और स्तंभों में विभाजित किया जाता है।
सारणीयन की विशेषताएँ
डाटा को व्यवस्थित करने की प्रणालीबद्ध विधि।
पंक्तियों और स्तंभों में जानकारी को प्रस्तुत करता है।
संख्यात्मक डाटा के विश्लेषण और तुलना को आसान बनाता है।
डाटा को अधिक व्यवस्थित और पढ़ने योग्य बनाता है।
मुख्य अंतर
वर्गीकरण में डाटा को समूहों में बांटा जाता है, जबकि सारणीयन में इसे तालिका के रूप में प्रस्तुत किया जाता है।
वर्गीकरण मुख्य रूप से आंकड़ों की पहचान और उनकी विशेषताओं पर केंद्रित होता है, जबकि सारणीयन आंकड़ों को व्यवस्थित तरीके से प्रदर्शित करने पर केंद्रित होता है।
वर्गीकरण बिना तालिका के भी किया जा सकता है, लेकिन सारणीयन में तालिका बनाना अनिवार्य होता है।
वर्गीकरण डेटा के मूल स्वरूप को पहचानने और उसे समूहों में रखने की प्रक्रिया है, जबकि सारणीयन इसका अधिक व्यवस्थित और सरल प्रस्तुतिकरण करता है।
इस प्रकार, वर्गीकरण और सारणीयन दोनों ही सांख्यिकीय विश्लेषण के महत्वपूर्ण चरण हैं, जिनका उद्देश्य आंकड़ों को व्यवस्थित और अधिक समझने योग्य बनाना है।
प्रश्न 06
हमारे पास कुल 20 सफेद (White) और 30 काले (Black) गेंदें हैं, यानी कुल गेंदों की संख्या:
𝑛
=
20
+
30
=
50
n=20+30=50
अब हमें दो स्थितियों में सफेद गेंद प्राप्त करने की संभावना निकालनी है:
(1) प्रतिस्थापन के साथ (With Replacement)
इस स्थिति में, पहली गेंद निकालने के बाद उसे वापस बैग में रख दिया जाता है, जिससे कुल गेंदों की संख्या हमेशा 50 बनी रहती है।
(2) प्रतिस्थापन के बिना (Without Replacement)
इस स्थिति में, पहली बार गेंद निकालने के बाद उसे वापस बैग में नहीं रखा जाता, जिससे कुल गेंदों की संख्या बदल जाती है।
निष्कर्ष
प्रतिस्थापन के साथ सफेद गेंद निकालने की संभावना
4/25
या 0.16 (16%) है।
प्रतिस्थापन के बिना सफेद गेंद निकालने की संभावना
38/245
या लगभग 0.155 (15.5%) है।
प्रश्न 07 सामान्य वितरण वक्र से आप क्या समझते हैं?
सामान्य वितरण वक्र का अर्थ
सामान्य वितरण वक्र (Normal Distribution Curve) एक सांख्यिकीय ग्राफ़ है, जो किसी डेटा सेट के वितरण को दर्शाने के लिए उपयोग किया जाता है। इसे गॉस वितरण (Gaussian Distribution) भी कहा जाता है। इस वक्र का आकार घंटी (Bell) के समान होता है, इसलिए इसे घंटी-वक्र (Bell Curve) भी कहा जाता है।
सामान्य वितरण वक्र की विशेषताएँ
घंटी के आकार का होता है – सामान्य वितरण वक्र का ग्राफ़ बीच में सबसे ऊँचा होता है और दोनों तरफ समान रूप से ढलान लिए होता है।
माध्य, माध्यिका और बहुलक समान होते हैं – इस वितरण में इन तीनों का मान एक ही बिंदु पर स्थित होता है।
संतुलित (Symmetric) होता है – वक्र का बायां और दायां भाग एक-दूसरे के समान होते हैं।
पूर्ण संख्या रेखा पर फैला होता है – यह वितरण
−
∞
−∞ से
+
∞
+∞ तक फैला होता है, लेकिन दूरस्थ बिंदुओं पर संभाव्यता बहुत कम हो जाती है।
मानक विचलन (Standard Deviation) के आधार पर डेटा बंटता है –
68% डेटा माध्य (
𝜇
μ) के ±1 मानक विचलन (
𝜎
σ) के भीतर होता है।
95% डेटा ±2 मानक विचलन के भीतर होता है।
99.7% डेटा ±3 मानक विचलन के भीतर होता है।
संभावना घनत्व फलन (Probability Density Function, PDF) – सामान्य वितरण को निम्नलिखित समीकरण से दर्शाया जाता है:
जहाँ,
𝜇
μ = माध्य (Mean)
𝜎
σ = मानक विचलन (Standard Deviation)
𝑥
x = चर (Variable)
सामान्य वितरण वक्र का महत्व
सांख्यिकी और गणित में महत्वपूर्ण – यह वितरण प्राकृतिक घटनाओं जैसे ऊँचाई, वजन, परीक्षा के अंक, आदि का विश्लेषण करने के लिए उपयोग किया जाता है।
त्रुटि विश्लेषण में सहायक – वैज्ञानिक और गणितीय प्रयोगों में होने वाली त्रुटियों का अध्ययन इस वक्र से किया जाता है।
संभाव्यता सिद्धांत में उपयोगी – यह वितरण विभिन्न संभाव्यता गणनाओं और पूर्वानुमानों के लिए उपयोग किया जाता है।
मशीन लर्निंग और डेटा साइंस में प्रयोग – कई डेटा मॉडलिंग और पूर्वानुमान विधियों में इस वक्र का उपयोग किया जाता है।
निष्कर्ष
सामान्य वितरण वक्र एक संतुलित और व्यवस्थित डेटा वितरण को दर्शाने वाला महत्वपूर्ण सांख्यिकीय उपकरण है। यह प्राकृतिक घटनाओं और वैज्ञानिक गणनाओं को बेहतर ढंग से समझने में मदद करता है।
प्रश्न 08 समग्र से आप क्या समझते हैं? इसके प्रमुख प्रकार कौन कौन से हैं?
समग्र का अर्थ
समग्र (Population) का अर्थ किसी अध्ययन या विश्लेषण के लिए उपयोग किए जाने वाले संपूर्ण समूह से है। यह उन सभी इकाइयों या तत्वों का समूह होता है जिनका अध्ययन या विश्लेषण किया जाता है।
उदाहरण के लिए, यदि किसी विश्वविद्यालय के छात्रों के परीक्षा अंकों का अध्ययन किया जा रहा है, तो विश्वविद्यालय के सभी छात्र समग्र कहलाएँगे।
समग्र के प्रमुख प्रकार
समग्र को विभिन्न आधारों पर वर्गीकृत किया जाता है, जिनमें मुख्यतः निम्नलिखित प्रकार होते हैं:
1. सीमित (परिमित) समग्र (Finite Population)
जब समग्र में इकाइयों की संख्या गिनने योग्य और निश्चित होती है, तो इसे सीमित समग्र कहते हैं।
उदाहरण:
किसी विद्यालय में 500 छात्रों का समूह।
किसी कारखाने में 200 मशीनों का सेट।
2. असीमित (अनंत) समग्र (Infinite Population)
जब समग्र में इकाइयों की संख्या इतनी अधिक होती है कि उसे गिना नहीं जा सकता, तो इसे असीमित समग्र कहते हैं।
उदाहरण:
पृथ्वी पर सभी जीवाणुओं की संख्या।
समुद्र में पाई जाने वाली मछलियों की संख्या।
3. वास्तविक समग्र (Real Population)
जब समग्र में मौजूद सभी इकाइयाँ वास्तविक होती हैं और उनका भौतिक रूप में अस्तित्व होता है, तो इसे वास्तविक समग्र कहते हैं।
उदाहरण:
किसी नगर की जनसंख्या।
किसी फैक्ट्री में कार्यरत श्रमिकों की संख्या।
4. आभासी समग्र (Hypothetical Population)
जब समग्र में मौजूद इकाइयाँ कल्पित या सैद्धांतिक होती हैं, तो इसे आभासी समग्र कहते हैं।
उदाहरण:
किसी सिक्के को अनगिनत बार उछालने पर प्राप्त संभावित परिणाम।
किसी मशीन के काम करने की संभावनाएँ।
5. सांख्यिकीय समग्र (Statistical Population)
जब समग्र में मौजूद सभी इकाइयों का अध्ययन सांख्यिकीय विधियों से किया जाता है, तो इसे सांख्यिकीय समग्र कहते हैं।
उदाहरण:
किसी शहर में 18-25 वर्ष की आयु के लोगों का वेतन वितरण।
किसी फैक्ट्री में उत्पादित वस्तुओं की गुणवत्ता का परीक्षण।
निष्कर्ष
समग्र किसी भी अध्ययन या अनुसंधान का मूल आधार होता है। इसके विभिन्न प्रकार होते हैं, जिनका चयन शोध की प्रकृति और आवश्यकताओं के अनुसार किया जाता है।

.png)






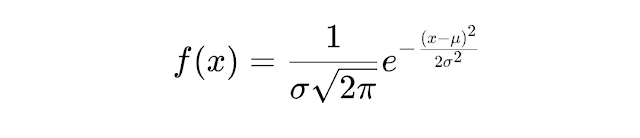
%20(31).jpg)

.jpg)

.png)
%20(31).jpg)

